Hare/Niemeyer
This method of distributing seats was named after the British legal professional Thomas Hare (1806 – 1891) and the German mathematician Horst Niemeyer (1931 – 2007). Hare developed the method in the second half of the 19th century. It was decided in 1970 that the method be used to man the committees and bodies of the German Bundestag after Niemeyer had suggested to do so.
At the elections to the 11th to 16th German Bundestag held from 1987 to 2005, the seats were apportioned according to the Hare/Niemeyer system; this also holds for the committees and bodies of the German Bundestag from 1969 to 1980. As to the German members of the European Parliament, the method was used from the third to the sixth European election in 1989 to 2004. Presently, the seats in the Länder parliaments of Bayern, Berlin, Brandenburg, Hessen, Mecklenburg-Vorpommern, Rheinland-Pfalz, Sachsen-Anhalt and Thüringen are distributed according to the system of Hare/Niemeyer (in Nordrhein-Westfalen until the latest election to the Land parliament in 2005).
The seats to be allocated to a party are calculated in two steps: First the number of second votes obtained by a party is multiplied by the total number of seats to be distributed and divided by the total number of all second votes to be considered. In a second step, the result is split up into the integral share and the residual. The integral shares are allocated to the parties in the form of seats. The remaining seats are allocated to the parties in the order of size of the residuals.
Formula:
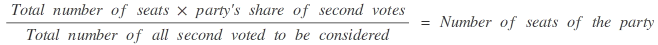
| Party | Calculation | Order of residuals by size | Seats thus to be allocated |
|---|---|---|---|
| Party A | 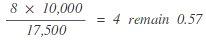 |
3. | 4 |
| Party B | 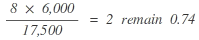 |
1. | 2 + 1 = 3 |
| Party C | 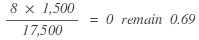 |
2. | 0 + 1 = 1 |
The example shows that in contrast to the calculation according to d’Hondt, the smallest party C will receive a seat and so the disadvantage smaller parties had is remedied by this method of distributing seats.
However, several paradoxes may occur with the Hare/Niemeyer method, for instance the Alabama paradox, as it is called. With the distribution of votes remaining unchanged, a party may lose a seat when the total number of seats to be apportioned is increased.
Last update: 1 January 2015